Keeping Particles in Line
Particle accelerators are tools of highest precision. The theory behind them however is remarkably simple.
The Basics
First off, there are many types of particle accelerators. But they all utilise the one effect science has found to reliably accelerate particles in vacuum: voltages acting on charged particles.
(And we are talking about making things go fastER! Already fast particles can come from many different sources, including space, radioactive decay and particle interaction.)
A voltage puts energy into charges changing their velocity. The higher the voltage, the faster the particles get.
Every charge creates a tiny voltage difference. How exactly that works isn't important right now. We only need this property to create our own voltages. By separating a lot of positive and negative charges in different containers, we can recover a high voltage between them.
Imagine two plates with nothing between them. When we put positive charges in one plate and negative charges in the other, the voltage resulting will add a velocity to all free charges between both plates. Postive charges gain velocity towards the negative plate and negative charges towards the positive.
In the macroscopic world, we rarely move around positive charges, but instead move around electrons. Any atom is made of it's core and electrons. The core and the electrons are oppositely charged.
As long as core and electrons are close togehter, their voltage differences overlap and we don't precieve them as charged. By separating them, we recover the voltage between them. And since atoms like to stick in their place and they only have one core, they tend to toss off electrons long before they start moving themselves. So when we "charge" something, we really talk about putting electrons in or pulling electrons out leaving the positively charged cores behind.
Metals are good charge-containers. Electrons can move freely through metals. If we make two plates out of metal, we can move charges between them by applying a voltage from a power source. This circuit is generally referred to as capacitor. If we have access to a high voltage source, we can build a simple accelerator.
A Simple Accelerator
To build a simple electron accelerator, we need two metal plates and some nonconducting material to hold them in place. We position them face to face and drill a hole at the very center through both plates. Over one hole we attach our experiment, e.g. a sample we want to examine. Over the other hole we attach our particle source.
A piece of wire we can heat very hot in vacuum is a good electron source. When metal is hot enough, some of the electrons will come out and we can accelerate them. And heating metal is as simple as building a light bulb: running high currents through some wire.
When we connect our voltage source to the plates, it takes electrons from one plate and puts them into the other. In theory, if we disconnect the plates from the voltage source, the charges would stay there without any additional work necessary. But there is no perfect insulator and over time, electrons would move slowly from one plate to the other. So we keep the voltage source attached.
To accelerate electrons, we heat the wire until it's hot enough. Some electrons will come out and by accident go through the hole. We get better results by charging the wire as well, so we connect that to a voltage source too.
As long as they are behind both plates, they will see the voltage of both plates overlap, similar to how an electron withtin the atom overlaps with the core. One plate adds velocity away from, while the other adds velocity towards to the plates. The overall force would be zero, so particles first have to come in between the plates.
Once an electron stumbled through the hole, it will gain velocity exactly perpendicular to them towards the plate with less electrons, ignoring the hole we drilled earlier. That is because there are equally many electrons on every side of the hole, and equally many missing electrons on every side of the opposing hole. An electron won't have any indicator weather to go right or left, just to get away from one plate and towards the other. If we drilled the holes precisely enough, any electron falling in one side will come out the other. A lot faster.
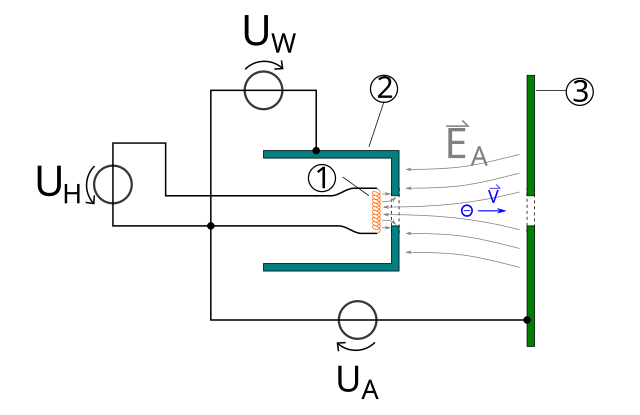
This simple particle accelerator is called an electron gun. For purely practical reasons it's better to use a cup as first plate, so the charged hot wire is shielded and doesn't disturbe the acceleration process.
- Hot wire
- Negative "plate" in form of a cup
- Positive plate with hole at center
All Us are a power source. UH is the power to heat the wire, UW and UA supply our acceleration voltage. Between the plates are arrows depicting the electric field, essentially how the voltage drops from one plate towards the other.
This simple device is already enough to have a lot of fun. It's the essential ingredient in electron microscopes and what powered old CRT monitors or by hitting a metal plate we can extract some x-rays or even build a metal 3D printer.
A Slightly More Complex Accelerator
The higher the voltage between the plates, the faster the electrons will come out. But for technical reasons, we can't create arbitrarily high voltages. Things would break down or become prohibitively expensive.
Placing accelerator after accelerator, though possible, would require many small voltage sources, which are usually even more expensive than a single big one. Not to mention we would effectively add up all their voltages, so we require very good isolation of our particle source and the experiment. We need to be clever.
For example by reusing a single voltage source over and over again. That way, we would still build accelerator after accelerator, but keep costs and voltage low by recycling.
In detail, many plates with holes in a row constitute many accelerators with missing voltage source. Connecting just two plates at a time, we activate just one accelerator. The first two plates operate exactly like the simple accelerator. A bunch of electrons enters and exits. While they fly through the exit plate, we rapidly unplug the voltage source and connect the next two plates. When the electron bunch flys through the next simple accelerator, it will work just like the first one. All we have to do now is repeat this process for all our plates and we get massively fast electrons.
We can switch the voltage source while the electrons pass through the hole in the plate without slwoing them down or knocking them off course. When replugging the plate the electrons fly through, we drain positive charges and fill it with negative ones. Since that happens on all sides of the hole at once, electrons in the hole see the same charges on all sides all the time. It doesn't matter how much they are pushed or pulled in no direction. switching the voltage therefore has no effect while the electrons are moving through the hole.
There is a simple upper limit to how fast this accelerator can make electrons go: How fast we can reverse high voltages. So again, we need to be clever to work around this problem.
A computer could do the switching for us. The problem here is the high voltage, which makes any switch, even a computer controlled switch, quite slow.
Reversing the voltage while the electrons fly through a thin plate is hard. Reversing the voltage while electrons fly through an elongated metal tube is easy. This way we have some more time to flip the switch.
To be super fast at switching, we want to wire up all plates in one place. What we will find is that we keep charging the plates in alternating fashion. So to make the switching faster, we can hook up every second plate to the same wire. This way, we are left with only two wires. Flipping them will flip the voltage in all plates. Now since we flip the voltage in all plates at the same time, we can even get some more electrons accelerated by accelerating several bunches at the same time but two tubes (= plates) appart.
The electrons get faster with every simple accelerator. To keep the time we have for switching constant, we need to build longer tubes after every stage. If we do this precise enough, we can dump the computer and instead use plain old alternating current to do the switching. Handling alternating current is much simpler from an engineering perspective than handling switches.

The animation shows how each tube is charged and, the green line above, how the voltage looks to the particle. Remember, only voltage differences change the velocity of a charged particle.
The takeaway here should be that alternating current is super simple but requires constant acceleration-times which require longer and longer accelerator tubes. But super long accelerators are unwieldy.
A Round Accelerator
Enter: magnets.
A magnetic field forces charges on circular (or coiling) path. We can use this to use the same tube over and over again.
The clever trick is the observation that an electron's circular path has to be bigger the faster it's moving.
As a result, the time an electron takes to complete one circle is always the same.
So what we could do is just take all our tubes and place them, bent, inside a magnetic field. By fiddling with the strength of the magnetic field, we can coil up our tubes until they all snuggle one another like a snake coiled up on itself. Electrons would start at the center and get faster and faster until they exit at the brim. This way we take advantage of the ever bigger circular paths.
But since the time for a single circle is constant, we can tune the magnetic field so the switching time is exactly one half-circle. The lengths of our tubes is tuned to our switching times. So now all our tubes take one half turn, resulting in all slits aligning and forming one slit splitting the coiled up snake in two.
Because we flip voltage every half-circle, all tubes connected together are on one half and the other tubes are in the other half. This allows us to remove the walls between the tubes.
Imagine a huge coin. Large enough that our fastest electrons can circle freely inside. Hollow it out. Slice it in halve. Place both halves facing each other roughly one hand width apart in a strong magnetic field. Put a particle source at the very center between both halves.
When particles exit the source, they see two charged "plates", so they move towards the positively charged half-coin. The magnetic field can be ignored for such small distances.
Once they are inside the "tube", they don't gain velocity but the magnetic field steers them. So they orbit around and want to exit the half-coin again. Before they do, the voltage flips. When the electrons exit, they see two charged "plates" and are driven away from the plate they just exited. This cycle repeats, until they are so fast, they don't fit inside our coin anymore.

Ernest Lawrance drew this for his patent of the cyclotron in 1934. On the left, you see the two half-coins 1 and 2. They are charged by a connected High Frequency Oscillator 4 (= AC-power). The ∓ and ± signify the two halfs are always charged oppoitely. What's not drawn is an extraction-tube for the High Speed Ions, which is technically required to shield them weird fields at the magnet's rim so they continue in a straight line. The line titled "Magnetic Field" is drawn where the field starts to diverge.
On the right the disk is viewed from the side. Here the magnet, 3, is depicted an it's magnetic field m is shown, including it's divergence on the edges. p indicates the particles' flight path, e the voltage applied to the particles and α the central plane. I guess j is supposed to be a 1, but I don't know what the arrows at the very top towards the center are supposed to signify.
This way, we can build a particle accelerator that would have been as long as some streets at the size of a fridge. So what happens if we make it bigger?
A Particle Round About
The coin-shaped accelerator will run into some problems when particles get too close to the speed of light. Relativistic effects take hold and correcting for them quickly gets very difficult.
A particle always gains the same energy when passing through an accelerator. Close to the speed of light, adding ever more kinetic energy doesn't add much more velocity.
Inside a magnetic field, the size of the circle a particle travels depends on it's energy, not it's speed. When our particles need to fly bigger circles at essentially the same speed, they can't all complete one circle at the same time anymore. Our coin-shaped accelerator won't work, because we based the concept on all particles taking the same time to travel a half-circle.
We need to be clever again.
At constant magnetic field, the time for a particle to complete one circle depends only on it's mass. According to relativity, mass is equal to energy. If we can manage to add the energy exactly equal to the mass of one electron during a single voltage flip, the electrons arrival times could be synchronised.
We can't build a device like this with two hollow half-coins. Instead, we need to build a tiny, simple accelerator consisting of two plates inside a magnetic field. Electrons exiting the accelerator will circle back to it's entry. Every time they fly through the accelerator, they take exactly one slow electron's circle time longer. That way, all electron bunches arrive synchronised with other bunches.
It looks quite similar, but here an extraction-tube is drawn in red which uses a small voltage to add some sideways velocity to the particle. The simple accelerator is at the top, connected to a high frequency voltage source.
The problem with this approach is that the simple accelerator needs to reach about 500 kV. Though quite doable, we still need to flip the voltage constantly at very high frequency. The particles need to arrive at the accelerator when the voltage is at it's highest value to be efficient. Since we want to accelerate our particles close to the speed of light, the time to flip is close to how long a ray of light would need to pass through an electron's circle. That is very little time and requires frequent switching.
However, this concept works for electrons only. Since we need to add the particles mass in energy with each passing, with higher particle mass we need to increase the voltage as well. Just protons would require to accelerate at around one giga volt. That is a trillion volts. That is a lot of voltage.
But even for electrons there is a simple size limit. The faster our electrons should be at the end of acceleration, the bigger circles they need to pass, the bigger our magnet has to be. At this point, we might as well give up.
A BIG Particle Round About
We want faster electrons. We want more particles. We need to go bigger!
Trying to build accelerators with magnets to have particles pass the same accelerator several times will soon find a very simple problem: focus.
Think about the distance electrons have to travel to pass through the accelerator. Even if the accelerator itself is quite small, the electrons still fly vast distances. Have you ever tried to focus a beam of light across town without any optics? That's what we are doing with our particles beams. We need some optics.
One bunch of electrons, though very tiny, is still spread out and every pass through a magnetic field spreads them out further by forcing them on different circles depending on their energy. Oh, and they are all of the same charge and therefore try to push eachother apart. Unless we can build tiny, powerful accelerators, cough, we need to focus the beam somehow.
Enter: more magnets.
First we need to split the one huge magnet into several smaller magnets, simply because one huge magnet is more expensive, harder to cool and simply not practical for our purposes. So instead we build magnets that turn the particles for some degrees, arrange them in a circle and let the particles fly between them. After each pass, we now have a particle beam we can manipulate, e.g. accelerate or do experiments with or focus again.
So how do we do focusing?
Even more magnets!
What would be great are magnets that don't effect the very centered electrons, but steer those at the side on a path inwards. Since magnetic fields curve the electrons path, that seems possible.
We just have to build two magnets next to each other, one on either side of the particle beam. One pushes them right, the other left, so that at the center they cancel out. The farther out a particle travels, the stronger it's pushed inwards, resulting in all particles being directed towards a single point behind the magnets.
Then all we have to do is build another pair of magnets that does the same thing with particles too far up or down. Simple, right? Wrong.
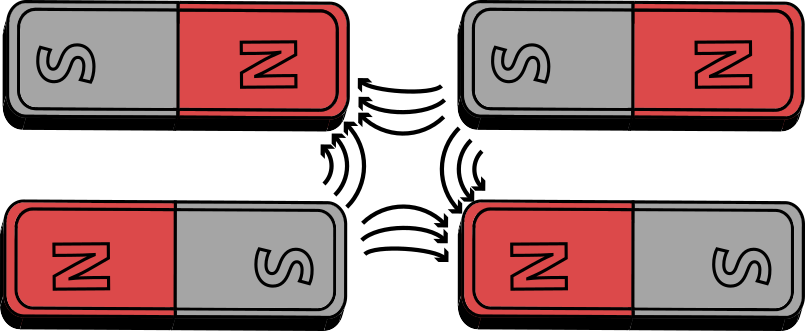
Two magnetic fields side by side interact and distort each other. Two opposing magnetic fields side by side are a special case called a quadrupole. And though a quadrupole does bend particles inwards in one direction, it spreads them out in the other by the same amount.
A schematic depiction of how a quadrupole forms. Though the sides may be distorted, at the center the magnetic field is curved equally horizontally and vertically.
Naively, we would say that moving inwards then outwards has no net effect. But that's not precisely what happens. What the magnets do is bend the particles' paths, so they move very little inward or outward. Instead, they are set on a trajectory which will land them further in or further out. Actually moving inwards or outwards happens after the quadrupole in free flight.
A quadrupoles magnetic field gradually changes from up to down or left to right, crossing zero at the very center of the particle beam. That means the closer the particles are to the beam center, the less steering force they experience. If we let the particles pass some distance before using a second quadrupole, the focused particles are close to the center and defocused particles are farther away. Thereby defocused particles will experience a stronger focusing force while focused particles experience a weaker defocusing force. If we choose the magnetic field strength and distance correctly, we can focus horizontally and vertically into the same point.
Using a focusing and defocusing lens to form a single focal point is actually well known in optics. They did us a favor by already working out the math of focal lengths, so all we need to do is plug in our special conditions and what we get is that the second lens needs to be twice as strong as the first one.
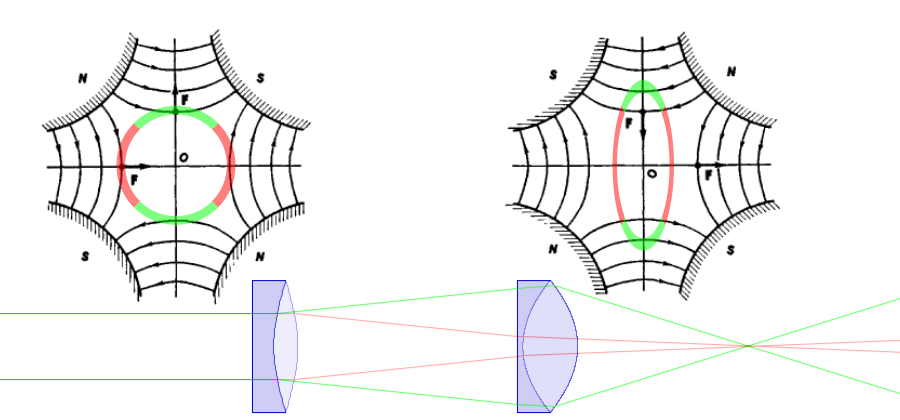
The top images show a front-view of the quadrupole as the particle beam sees it, with a colored ring tracing the brim of the beam. Red and green signify horizontal and vertical portions of the beam. Below, the vertical and horizontal edges of the beam are shown in a side view. As you can see, they end up passing through the same point. (The effect of the magnetic fields are shown for positively charged particles, electrons behave inversely.)
Usually though, even more complex magnetic fields are used. A quadrupole is a great thing, but particles of different energies are affected differently. Add another pair of magnets forming a sextupole and that problem can be fixed. And having all particles pass through one point isn't enough, we want them to approach in the same angle of incidence. Add another quadrupole (or sextupole) and that's possible as well. But since we have our particles go in circles, there isn't just one point where they should be focused but rather constantly kept close together. Sprinkle some linear algebra on top, and you can calculate a constantly focused beam.
Finally!
We did it! We've got super fast particles waiting for our experiments. With this much energy, we can tap into a whole new realm of physics. With some puny electrons we could observe the structure of tiny crystals. With particle beams we can observe the structure of subatomic particles. Sort of.
It's much more difficult to take "pictures" at this scale. Essentially impossible. When we observe scattered electrons, we just need to look at the exact angle they came from to calculate a picture. When we smash particles to pieces, we need to look at the fragments very carefully to get at least some information about the structure of the initial particle. If it had a charge-distribution, they will scatter slightly differently. That's why particle colliders [need][cms] to be that huge, so they can observe all fragments scattering in all directions. And that's if they observe anything at all.
We accelerate particles in bunches. One bunch has some several thousand particles. It's much more a loose cloud of particles. When this cloud hits a hard wall, there are so many atoms in that wall that every particle will find an atom eventually. But that's quite inefficient, because most of our particle's energy will be conserved in kinetic energy in the particles scattering off. To direct most energy into the particle reaction, we need to have two bunches heading for each other straight on. But since bunches are quite loose, nearly all particles will miss. It will take many bunches to observe even a single reaction.
That's why the LHC has two particle beams. But even when collisions happen, most of the time they are two particles slightly touching and not head on. So we need to observe many collisions until we find an interesting one. Now there is the problem of building collision detectors. But that's another chapter for a later day.
Shiny Electrons!
The following isn't necessarily important, but it's interesting and I'm too lazy to write another post about it.
There is a bunch of cool experiments we could try with fast particles, but the very first one is actually a bit of a problem for circular accelerators. Particles inside a magnetic field will loose energy. Not because of resistance in the classical sense, they are in vacuum, but because of radiation.
Whenever a charge changes velocity, some energy is lost as radiation. We actively use that effect in X-ray tubes: An electron beam hits a target, thereby slowing the electrons down instantly. This massive (negative) acceleration releases a lot of radiation. The same thing occurs inside a linear accelerator, where we accelerate electrons to ever higher velocities. And though magnetic fields don't change particles' speeds, they do direct them and thereby change their velocity. That's still acceleration. And actually the worst kind. Thanks to, you guessed it, relativity.
So firstly, radiation always shoots out sideways to any acceleration. Imagine a charge on a rope. If you pull the rope and accelerate the charge, the radiation is released in the shape of an umbrella. Far below the speed of light, it doesn't matter in what direction you pull the rope, the radiation will always come out sideways.
But the speed of light does weird things to radiation. Essentially, at relativistic speeds radiation released sideways is dimmed, even more so backwards, while radiation released forwards is that much brighter. Conservation of energy is still in effect, so that extra radiation is powered by extra losses of kinetic energy of the particle. Pulling the rope in the charge's direction of flight releases the same umbrella of radiation, only smaller, so less energy is lost. However, pulling the rope on our charge sideways will form a high radiation beam in the direction of flight, costing much more energy. On the other hand, we just built a brilliant torch light.
A Brilliant Bunch
In some cases, we want brilliant light. Material properties, surface phenomena and dark rooms react quite revealing to brilliance. But for fast particles, this is plain lost energy. We need to minimise these losses if we want to conduct some particle physics.
There are two things we can do to control that effect. First and foremost, we can build particle roundabouts as straight as possible. So either plain linear accelerators, or very huge roundabouts. Usually, this would be the point to be clever, but so far nobody was. It seems pretty essential physics: Turning particles is acceleration and costs energy. Maybe building very efficient accelerators could overcompensate that energy loss, but right now, it's cheaper to build huge circles. If you find a way to be clever, you are probably in for a Nobel Price.
The only trick we know is using heavier particles. The heavier a particle is, the slower it can be while still carrying the same energy. It's a drop on a stone, but it's something.
On the other hand, we could do the opposite and build brilliant lights. These are called synchrotrons. In a synchrotorn, electrons are used since they are very light. Behind every magnet the light is used in a beam line to do experiments. Turning electrons are a unique light source, because they are easily tuneable and shine bright even in the x-ray spectrum. A single magnet, however, causes them to release a whole range of colors. To dial in a specific wavelength, one possibility is to wiggle the beam left to right with many alternating magnetic fields. This device works by releasing radiation with every tight turn the electrons are forced to take. Light from previous turns shines on electrons taking the next turns. This light resonates with the electrons and eases radiation of the same color, so more radiation of a single color is released.
Kicking it up a notch is the free electron laser. In a wiggler, a color is roughly dialed in by choosing the right turning radius and distance. Though it helps with dialing in a specific color, the electrons still shine bright in adjacent colors. But we can use the same effect that made wigglers more efficient: radiation eases the release of the same color.
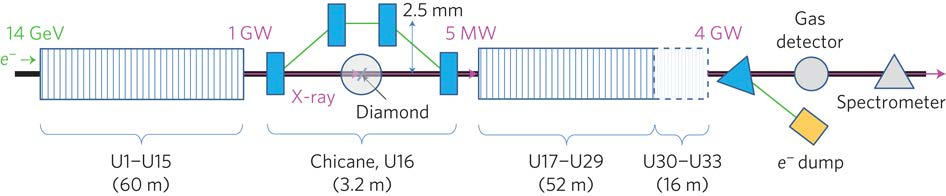
What you see here are two wigglers with a side-track for the electrons in between. The light from the first wiggler is filterd with a diamond, the filtered light then is amplified by the second wiggler. Behind that assembly the electrons are removed and some experiments conducted.
A free electron laser consists of two wigglers. The first is used to shine roughly one color on a set of filters. The filters clean up the radiation by removing all the color we don't want. That radiation is directed into the next wiggler, amplifying that radiation and resulting in massive radiation of a very narrow color.
So there you go. That's how billion dollar research facilities work. Now if anybody could tell me what magic drives a microwave, I might explain that next time.